高中化學學習上,我們常會碰到有關熔沸點比較的問題,而有鑑於其觀念需要眾多觀念
的整理與活用,故在這裡做了一些簡述,希望能幫助大家!!
分子間作用力:
依照分子(離子)間的作用力強度,我們可以區分為以下兩種:
(1)化學鍵(強度較強)
※什麼是電子海-金屬鍵的模型
電子海模型係指金屬原子可將價電子互相共用形成電子海,而原子核則浸泡在電子海裡面。有點文言? 那我們就來看圖吧!
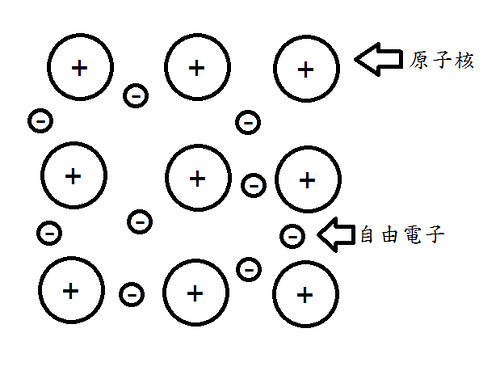
依圖可知,被共用出來的價電子可在原子核之間移動,而這時電子可以比擬成膠水,其與原子核之間的靜電吸引力可以穩固結構(克服核之間的排斥力),也使得金屬具有高度柔軟性,不易碎裂的特質。
(2)分子間作用力:
最常用來描述分子間(內)的作用力為凡得瓦力(van der Waals' force),又可分為三類:
|
|
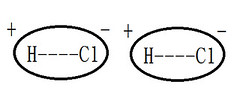
偶極-偶極力 (dipole-dipole interaction) |
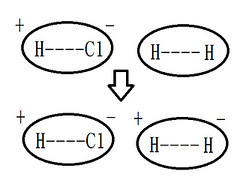
偶極-誘導偶極力 (dipole-induced dipole interaction) |
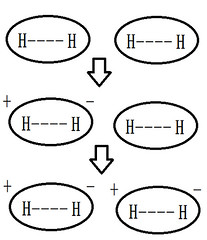
倫敦分散力 (London dispersion Force) |
|
形成原因 |
極性分子因偶極矩互相造成的靜電引力 |
極性分子極化非極性分子而產生的靜電引力 |
非極性分子間因為電子暫時分布不均勻而部分極化所產生之作用力 |
|
圖解 |
 |
 |
 |
※上述之偶極-偶極力若是由氫原子(H)接在F、O、N等原子上,則可形成強度較強之分子間作用力-氫鍵
※極性分子間並未只有偶極-偶極力,而應該也有倫敦分散力,請別搞混了!
物質間的分類:
物質的分類可以區分為以下幾種,在釐清化合物與作用力之間的關係尤其重要:
|
|
離子晶體 |
分子晶體 |
網狀晶體 |
金屬晶體 |
|
作用力 |
離子鍵 |
凡得瓦力 |
共價鍵 |
金屬鍵 |
|
達熔點時所需破壞作用力 |
離子鍵 |
凡得瓦力 |
共價鍵 |
金屬鍵 |
|
達沸點時所需破壞作用力 |
離子間庫倫靜電力 |
凡得瓦力 |
- |
金屬鍵 |
|
實例 |
離子化合物 |
分子化合物: AlCl3、Al2Cl6、LiClO4、LiCl、BeCl2、CO2、C60 |
SiO2、Si、B、鑽石、石墨、SiC、奈米碳管 BN、網狀聚合物 |
金屬原子 |
有了以上的觀念釐清後,我們可以利用這些概念去解決很多問題,例如比熔點、沸點、溶解度等....
但要注意,化學這一門學問,還是以實驗結果為上,並沒有一套理論能真的100%預測成功,雖然可能已經很接近了)
◎熔點、沸點? 到底該怎麼比?
在往下看之前,先問各位一個問題,要怎麼比一個化合物的熔沸點?如果你的答案是氫鍵>分子量……(可能有7成都是這樣回答?),那就表示你該看看這份手稿
有關於熔沸點的比較,第一步不是直接我會因為我有背,而是先看看到底達到熔、沸點時,我要克服的是甚麼樣的化學鍵或作用力,這在上表有整理到。
而一般來說,不同型的化合物間的熔沸點比較,有粗淺的以下關係:
|
網狀固體> IIAO> SiO2>2價離子化合物>過度金屬(汞例外)>1價離子化合物>典型金屬>分子化合物 |
依照這樣的比法,我們要做的應該是先分類,看看題目給了我們甚麼類型化合物,再依照各化合物的比法繼續下去,以下我們就來討論看看:
※離子化合物之熔沸點:
|
離子之熔沸點比較:熔點:離子鍵/沸點:庫倫靜電力 1. 1:1型(AB型)
實例:MgO>NaCl II. 同價數時,比半徑(∵庫倫靜電力∝1/r) 實例:LiF>NaCl 2. 非1:1型(ABx型)
實例: MgCl2>CuCl2 II. 不同型→外圍接鹵素越多,熔沸點越小 實例: NaCl>MgCl2>、SnCl2>SnCl4 ※進階討論-法楊規則(極化效應) 我們先以NaCl的離子鍵來開始我們的討論:
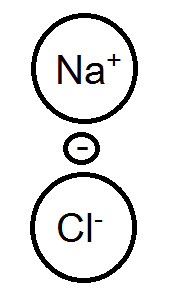
首先我們知道,NaCl的離子鍵是由Na丟一顆電子給Cl形成Na+與Cl-離子,而由其離子間的庫倫靜電力所形成的 而這時Na丟給Cl的電子,在圖上我們可以看出,會受到Na+的正電荷吸引力,所以其實電子並不是100%給Cl。 我們再來看看MgCl2的情況:
此時電子所受到Mg2+電荷吸引力比Na+大,所以電子給得更不完全,造成共價性上升,所以熔沸點反而是降低的。 |
※金屬原子之熔沸點
|
金屬元素之熔沸點比較(熔點、沸點:破壞金屬鍵) 1. 同週期元素(∝Q∵V差不多) 實例:Na<Mg<Al 2. 同族元素(∝1/V ∵Q一樣) 實例:Li>Na>K>Rb>Cs、Be>Mg 實際上,不同金屬元素在比熔沸點之前,應該要注意堆積方式 一不一樣,以2A族為例,Be、Mg都屬於六方最密堆積,故可以直接用 以上規則來判斷,但若是Mg與Ca來比,就不能用上面的規則來判斷, 但各位只要知道2A族是Be最大、Mg最小即可 而1A族元素因為都是體心立方堆積,所以沒有以上問題。 |
※共價化合物之熔沸點:
在比熔沸點之前,我們應該要知道,共價化合物又可以分為網狀固體與分子化合物,兩者在熔沸點上可說是天差地遠,所以看到題目後要仔細想想,到底它給的化合物屬於哪一類再開始做比較,最明顯的差異就屬SiO2與CO2了
|
共價化合物之熔沸點比較:分子化合物:熔點:凡得瓦力/沸點:凡得瓦力 網狀共價固體:熔點:共價鍵/沸點:-
比法:
※電子數(分子量)與凡得瓦力強度的關係: 凡得瓦力可以想成是萬有引力,任何物質只要擁有質量都會有萬有引力,且質量越大,此力越強(比較好記憶)。 但若要探究真實的影響原因,我們可以先從上面表格的倫敦分散力開始講起,在討論倫敦分散力時,我們說過起因是電子突然分布不均所造成的暫時極化現象,而若電子數越多,這種機率就會越高,且強度會增大,故造成凡得瓦力強度上升。而說到這裡,我們知道不管是極性分子還是非極性分子,都會受倫敦分散力影響,所以電子數的考量是不可或缺的
※對稱性與熔點的關係 熔點是指某一化合物從固體變成液體時所需加熱到的溫度,而在分子晶體的討論上,我們知道,其固體的形成原因就是因為其分子間有凡得瓦力,造成分子堆積。 若要使固體熔化,我們需要破壞其整齊排列的堆積結構,而通常對稱性越高的分子,其排列整齊度越好,所以較難破壞其結構,熔點較高。 同樣的討論方法也可用在溶解度上,因為在溶解的過程中,也是需要破壞其晶體結構才能溶在溶劑中,所以通常分子的熔點與溶解度在比較的因素上會差不多。
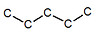
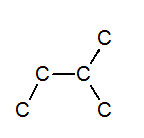
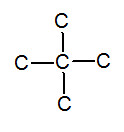
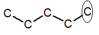
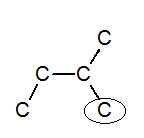
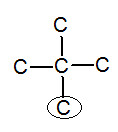
※接觸面積與沸點的關係: 以下我們考慮正戊烷、異戊烷、新戊烷圈起來的碳 正戊烷 異戊烷 新戊烷 由圖可見,三分子圈起來的碳與其同類其他分子的碳平均距離大小為正>異>新戊烷,又因距離越近,凡得瓦力越大,所以接觸面積才與凡得瓦力有關。 |
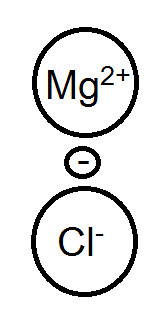


 留言列表
留言列表

