金屬原子的堆積與其他你所需要知道的觀念!!!!
I. 金屬原子堆積方式討論
我們知道金屬晶體的結構是有規則且無限延伸、各項同性的,因此可以利用此項性質,將金屬的堆積結構看成是一個個的單位晶格 (unit cell) 排列而成的,而這些晶格由大小相同的原子(看成一顆顆半徑相同的圓球)所填充而來。常見的晶格排列方式有以下幾種,我們可以分點來討論:
l 最密堆積(Closet Packing)
在深入了解各種堆積方式之前,我們可以先了解要如何在空間中做最有效率的堆積方式?以下我們分層討論:
<第一層>
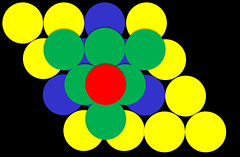
首先,我們只考慮一個平面,此時我們有兩種堆積的方式,如圖:


若我們仔細觀察這兩種堆積方式,我們可以看出其兩者有個差異
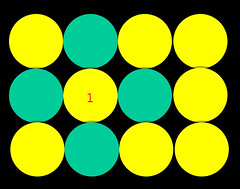
我們將目標放在其上有標號1的圓球,會發現左邊的堆積方式周圍會有4個圓球;而右邊的堆積方式周圍會有6個圓球。由此可見,右邊的堆積方式是較緊密的(圖上可能比較難想像,但無限延伸之後就會有差了)。
所以,我們將右邊的堆積方式稱為最密堆積,我們常簡稱為a
<第二層>
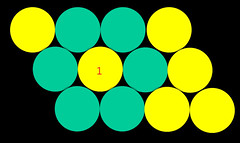
我們已經了解在單一平面上最密堆積的結構方法,接下來,我們可以依序討論第二層在空間上的排列方式。
第二層的堆積方法其層內的圓球也要滿足與第一層相同的堆積方法,而圓球為了滿足最密堆積,勢必要堆積在第一層圓球與圓球中間的空隙中,如圖:
我們常簡稱第二層(綠色層)為b
<第三層>
第三層相對第二層,有比較多種選擇,而根據第三層選擇的堆積方式不同,也會有不同的結構產生,可分為兩類,我們分別來討論;
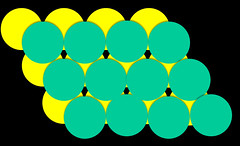
(1)面心立方堆積結構(Face Centered Cubic Packed Structure, 縮寫:fcc)
其選擇的第三層堆積方法是將圓球安插在第二層(b)的圓球間,如圖:
我們叫這種第三層為c,是故面心立方的堆積方法為abc重複
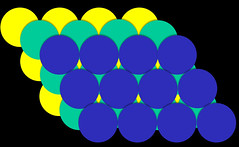
而我們擷取單位晶格的方式,可由以下圖片來說明
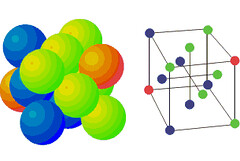
(圖片來源: http://faculty.uml.edu/ndeluca/84.334/topics/topic2.htm)
(2)六方最密堆積結構(Hexagonal Closest Packed Structure, 縮寫:hcp)
其選擇的第三層堆積方法同第一層(a),如圖:

此圖中的白色框為第三層的圓球,與第一層重疊。
是故我們說六方最密堆積的堆積方法為aba重複
而我們擷取單位晶格的方式,可由以下圖片來說明
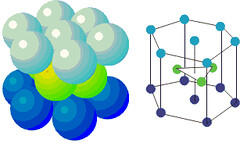
(圖片來源: http://faculty.uml.edu/ndeluca/84.334/topics/topic2.htm)
l 其他堆積方式:
除了最密的堆積方式之外,還有其他種堆積方式,以下我們就同樣以圖形來說明!
(1)簡單立方堆積(Simple Cubic Packing, 縮寫:SC)
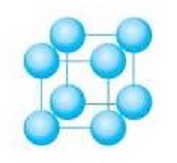
(圖片來源: http://www.51wendang.com/doc/81c02e7a4cda99eec1b6d18a)
(2)體心立方堆積(Body Centered Cubic Packing, 縮寫:BCC)
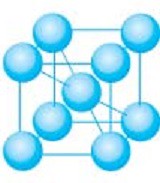
(圖片來源:
http://www.jxteacher.com/taihe/column30549/4c680477-468d-421a-9599-f0f72443593f.html)
- II. 各種晶型所需要知道的各種計算!
在了解各種晶型的堆積方式之後,可能你會有個疑問,例如,我們常說的最密堆積到底是有〝多緊密〞;原子半徑與晶格大小的關係為何……,以下就來為各位一一解答。
l 原子填充率(Atomic Packing Factor, 縮寫:APF)
此名詞定義為: ![]() ,算出此項數值,我們就可以知道各種晶型在空間的使用效率為何。
,算出此項數值,我們就可以知道各種晶型在空間的使用效率為何。
(1)面心立方
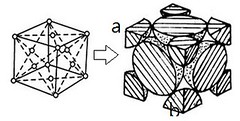
(圖片來源:http://cs.scutde.net/T21Courses/2102-rpwm5n8hi1/main/page/c010200.html)
首先,我們假設此正方形晶格邊長為a,原子半徑為R,根據此圖,我們
可以知道以下關係:

而一個單位晶格所含原子數為:
![]()
故APF=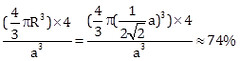
很神奇吧,就算是最密堆積在空間的使用上也只不過74%而已!
(2)體心立方
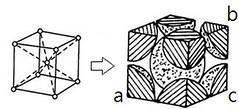
(圖片來源:http://cs.scutde.net/T21Courses/2102-rpwm5n8hi1/main/page/c010200.html)
首先,我們假設此正方形晶格邊長為a,原子半徑為R,根據此圖,我們可以知道以下關係:

而一個單位晶格所含原子數為:
![]()
APF=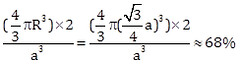
(3)六方最密
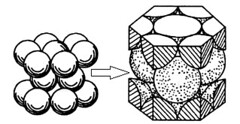
六方最密在計算上是最繁瑣的,不過我們還是來嘗試看看吧!
首先我們一樣假設原子半徑為r,但這次我們改假設此晶格的高為h
若仔細觀察,我們知道第一層中心原子與第二層3個原子可形成正四面體
是故我們知道:
![]()
此晶格所占原子個數:
![]()
此單位晶格體積=![]()
APF=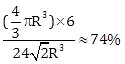
l 整理
|
晶型 |
縮寫 |
邊長關係 |
單位晶格原子數 |
APF |
距離最近原子數 |
例子 |
|
面心立方 |
FCC |
|
4 |
74% |
12 |
Ca、Sr、Al |
|
體心立方 |
BCC |
|
2 |
68% |
8 |
1A族、Ba、Ra |
|
六方最密 |
HCP |
- |
6 |
74% |
12 |
Be、Mg |
|
簡單立方 |
SC |
|
1 |
52% |
6 |
Bi |


 留言列表
留言列表

